Logaritmo decimal
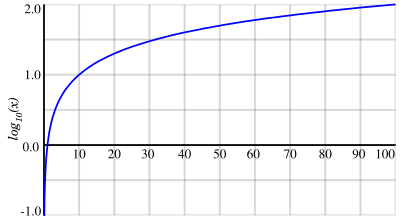
En matemáticas, se denomina logaritmo decimal, logaritmo común o logaritmo vulgar al logaritmo cuya base es 10, por lo tanto, es el exponente al cual hay que elevar 10 (exponenciación) para obtener dicho número. Se suele denotar como log10(x), o a veces como log(x), aunque esta última notación causa ambigüedades, ya que los matemáticos usan ese término para referirse al logaritmo complejo. El logaritmo decimal fue desarrollado por Henry Brigges.
El logaritmo natural suele ser conocido normalmente como logaritmo neperiano, aunque esencialmente son conceptos distintos. Para más detalles, véase logaritmo neperiano.
En matemáticas se denomina logaritmo natural o informalmente logaritmo neperiano al logaritmo cuya base es el número e, un número irracional cuyo valor aproximado es 2,7182818284590452353602874713527. El logaritmo natural se suele denominar como ln(x) o a veces como loge(x), porque para ese número se cumple la propiedad de que el logaritmo vale 1.
El logaritmo natural de un número x es entonces el exponente a al que debe ser elevado el número e para obtener x. Por ejemplo, el logaritmo de 7,38905... es 2, ya que e2=7,38905... El logaritmo de e es 1, ya que e1=e.
Desde el punto de vista del análisis matemático, puede definirse para cualquier número real positivo x>0 como el área bajo la curva y=1/t entre 1 y x. La sencillez de esta definición es la que justifica la denominación de «natural» para el logaritmo con esta base concreta.2 Esta definición puede extenderse a los números complejos.
El logaritmo natural es entonces una función real con dominio de definición los números reales positivos:
loge es el logaritmo «natural» porque automáticamente surge, y aparece más comúnmente, en matemáticas. Por ejemplo, consideremos el problema de derivar una función logarítmica:
Sentidos adicionales de esta naturalidad no hacen uso del cálculo. Como ejemplo, tenemos un número de series simples relacionadas con el logaritmo natural. Además de que Pietro Mengoli y Nicholas Mercator lo llamaron logarithmus naturalis unas décadas antes de que Newton y Leibniz desarrollaran el cálculo.
Formalmente, la función ln(x) se define para valores reales positivos, como el área bajo la gráfica de 1/t entre 1 y x. Esta área corresponde a una integral:
Mediante esta definición es inmediato comprobar que esta función cumple la propiedad fundamental de todo logaritmo:
El número para el cual esta función vale 1 resulta ser el número e. Por lo tanto, ln es el logaritmo con base e, o sea, la función inversa de ex.
El logaritmo natural puede ser integrado utilizando el método de integración por partes. Los detalles se dejan al lector.
Propiedades características
Observando la siguiente progresión geométrica.- Los únicos números de este sistema cuyos logaritmos son enteros son las potecia de diez.Así:
- El logaritmo de todo número que no es potencia de de 10 no es un entero, sino una fracción propia o un entero más una fracción propia o mantisa
- Como
 y
y  , los números comprendidos entre 1 y 10 tendrán un logaritmo mayor a 0 y menor que 1; su logaritmo será un fracción propia.
, los números comprendidos entre 1 y 10 tendrán un logaritmo mayor a 0 y menor que 1; su logaritmo será un fracción propia.
- Como
 y
y  ,
los números comprendidos entre 10 y 100 tendrán un logaritmo mayor a 1 y
menor que 2; su logaritmo será 1 más una fracción propia.
,
los números comprendidos entre 10 y 100 tendrán un logaritmo mayor a 1 y
menor que 2; su logaritmo será 1 más una fracción propia.
- Como
 y
y  ,
los números comprendidos entre 100 y 1000 tendrán un logaritmo mayor a 2
y menor que 3; su logaritmo será 2 más una fracción propia.
,
los números comprendidos entre 100 y 1000 tendrán un logaritmo mayor a 2
y menor que 3; su logaritmo será 2 más una fracción propia. 
Parte entera y mantisa
Se puede resumir de lo anterior que los logaritmos decimales tienen, en general, una parte entera y una parte fraccionaria.- Se denomina característica a la parte entera del logaritmo.
- Se denomina mantisa a la parte fraccionaria (que puede ser cero).
- La característica de un número comprendido entre 1 y 10 (excluido este) es cero. Es lógico ya que
 y
y  entonces los números comprendidos entre 1 y otro menor que 10 serán decimales, con entero 0, que es su característica.
entonces los números comprendidos entre 1 y otro menor que 10 serán decimales, con entero 0, que es su característica. - La característica de los números superiores o iguales a 10 será un número igual a la cantidad de cifras menos 1 del mencionado número. Así para 10, 20 o 30 su característica es 1; la de 150 es 2, etc.
- La característica y mantisa de los logaritmos superiores a 1 será positiva.
- La característica de los logaritmos entre 0 y 1 será negativa y su mantisa positiva.
Logaritmo natural
| Logaritmo natural | ||
|---|---|---|
 |
En matemáticas se denomina logaritmo natural o informalmente logaritmo neperiano al logaritmo cuya base es el número e, un número irracional cuyo valor aproximado es 2,7182818284590452353602874713527. El logaritmo natural se suele denominar como ln(x) o a veces como loge(x), porque para ese número se cumple la propiedad de que el logaritmo vale 1.
El logaritmo natural de un número x es entonces el exponente a al que debe ser elevado el número e para obtener x. Por ejemplo, el logaritmo de 7,38905... es 2, ya que e2=7,38905... El logaritmo de e es 1, ya que e1=e.
Desde el punto de vista del análisis matemático, puede definirse para cualquier número real positivo x>0 como el área bajo la curva y=1/t entre 1 y x. La sencillez de esta definición es la que justifica la denominación de «natural» para el logaritmo con esta base concreta.2 Esta definición puede extenderse a los números complejos.
El logaritmo natural es entonces una función real con dominio de definición los números reales positivos:
Historia
La primera mención del logaritmo natural fue dada por Nikolaus Mercator en su trabajo Logarithmotechnia publicado en 1668, a pesar de que el profesor de matemáticas John Speidell ya lo había hecho en 1619 recopilando una tabla sobre valores del logaritmo natural. Fue llamado formalmente como logaritmo hiperbólico,puesto que sus valores correspondían con los del área hallada bajo la hipérbola. A veces también se refiere al logaritmo neperiano, a pesar de que el significado original de este término es ligeramente diferente.Origen del término logaritmo natural
Inicialmente, y desde que el sistema decimal se volvió el sistema de numeración más común, podría parecer que la base 10 fuese más «natural» que la base e. Pero matemáticamente, el número 10 no es particularmente significativo. Su uso cultural—como base numérica para muchas sociedades—probablemente surge del típico número de dedos humanos. Otras culturas basaron sus sistemas de numeración eligiendo diversas bases como 5, 8, 12, 20, y 60.loge es el logaritmo «natural» porque automáticamente surge, y aparece más comúnmente, en matemáticas. Por ejemplo, consideremos el problema de derivar una función logarítmica:
Sentidos adicionales de esta naturalidad no hacen uso del cálculo. Como ejemplo, tenemos un número de series simples relacionadas con el logaritmo natural. Además de que Pietro Mengoli y Nicholas Mercator lo llamaron logarithmus naturalis unas décadas antes de que Newton y Leibniz desarrollaran el cálculo.
Definición
La función logaritmo natural ln:R+→R se define como: |
 ,
,
| Demostración |
Propiedades
El logaritmo natural cumple con las propiedades generales de los logaritmos, así como las identidades logarítmicas; Aparte de las propiedades generales, se destacan las siguientes:-
- (véase logaritmo complejo)
El logaritmo natural en integración
El logaritmo natural permite la integración sencilla de las funciones de la forma g(x) = f '(x)/f(x): una primitiva g(x) viene dada por ln(|f(x)|). Esto es debido a la regla de la cadena y también a lo siguiente:El logaritmo natural puede ser integrado utilizando el método de integración por partes. Los detalles se dejan al lector.











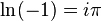


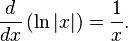









Una explicación bastante clara. Muchas gracias por compartir tus conocimientos con todos.
ResponderEliminarCASINO HOTEL 3rd ST, Suite 202, Las Vegas, NV - Mapyro
ResponderEliminarFind the BEST & NEW 의정부 출장안마 CASINO HOTEL 3RD 동두천 출장마사지 ST in Las Vegas, NV. See map 춘천 출장샵 and reviews. Search for other Casinos 전라북도 출장안마 near Casino 광주 출장샵 Hotel.